Условия устойчивости работы двигателя

Принцип работы системы курсовой устойчивости автомобиля

Рубрика: Технические науки

Дата публикации: 15.01.2017 2017-01-15

Статья просмотрена: 1464 раза

Библиографическое описание:

Швалёв, С. Г. Принцип работы системы курсовой устойчивости автомобиля / С. Г. Швалёв. — Текст : непосредственный // Молодой ученый. — 2017. — № 2 (136). — С. 213-216. — URL: https://moluch.ru/archive/136/38240/ (дата обращения: 16.09.2021).

Учитывая всю непостоянность погодных условий при эксплуатации автомобилей, актуальным становится вопрос курсовой устойчивости автомобиля.

Ключевые слова: ESP, датчик, безопасность, курсовая устойчивость

ESP — активная система безопасности автомобиля, позволяющая предотвратить занос посредством управления компьютером момента силы колеса (одновременно одного или нескольких).

Основной задачей системы электронной стабилизации ESP является выравнивание автомобиля в ту сторону, куда направлены передние колеса. На автомобиле установлены датчики продольного и поперечного ускорения кузова, датчики угловых скоростей всех четырех колес, датчик положения педали тормоза, датчик положения рулевого колеса, датчик давления в главном тормозной цилиндре, насос с разделенной системой управления тормозными магистралями колес и электронным блоком управления всем этим.

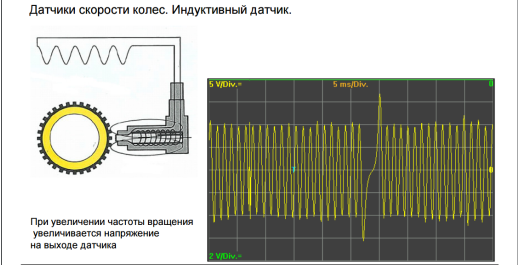
Рис. 1. Принцип работы датчика скорости колёс

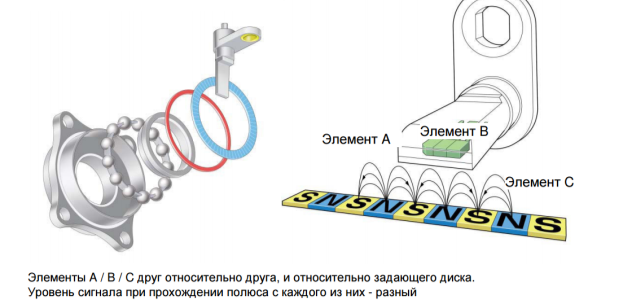
Рис. 2. Активный датчик частоты вращения колеса

Блок управления делает опрос 4-х датчиков вращения колес. Опрашивается также положения рулевого колеса и датчик продольного и поперечного ускорения автомобиля.

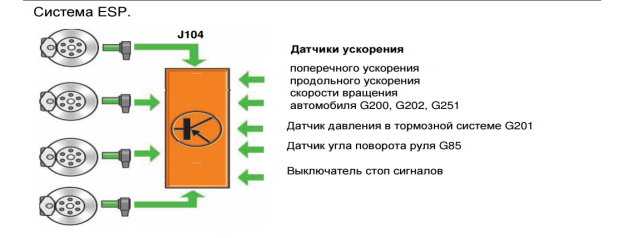
Рис. 3. Датчики ускорения

Все данные обрабатываются электронным блоком управления, как только данные с одного или нескольких датчиков превысят критические значения, записанные в базе данных блока управления, программа согласно заданному алгоритму действий начнет выправлять траекторию автомобиля посредствам управления тормозной системой (изменение скоростей колес) и системой подачи топлива, что приводит к выравниванию автомобиля в направлении колес.

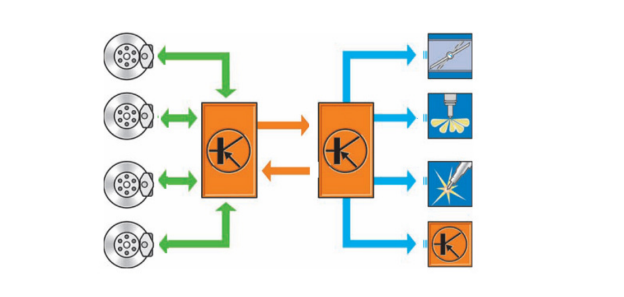
Рис. 4. Управление торможением колес и моментом привода

Подтормаживанием отдельных колес ESP создаёт разворачивающий момент. Этот момент направлен противоположно нежелательному разворачивающему моменту и стабилизирует его движение по заданному курсу (курс определяется датчиком положения рулевого колеса). При условии невозможности коррекции только с помощью направленного торможения — изменяется крутящий момент двигателя.

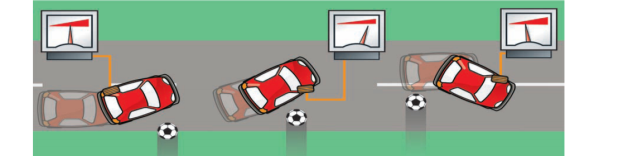
Рис. 5. Подтормаживание отдельных колес

С применением системы курсовой устойчивости значительно повышается безопасность автомобиля. Эксперты называют систему ESP самым важным изобретением в сфере автомобильной безопасности после ремней безопасности. Она обеспечивает водителю лучший контроль над поведением автомобиля, следя за тем, чтобы он перемещался в том направлении, куда указывает поворот руля. По данным американского Страхового института дорожной безопасности (IIHS) и Национального управления безопасностью движения на трассах NHTSA (США), примерно одна треть смертельных аварий могла бы быть предотвращена системой ESP, если бы ей были оснащены все автомобили.

Устойчивость работы электропривода

Дата добавления: 2014-10-07 ; просмотров: 3624 ; Нарушение авторских прав

Электропривод представляет собой электромеханическую систему, которая должна работать устойчиво.

Примером устойчивой системы является детская игрушка «Ванька-встанька».

Если «Ваньку» наклонить, а затем убрать руку, игрушка качнется несколько раз в разные стороны, а затем замрет, вернувшись в прежнее положение.

Точно так же работают устойчивые системы.

Рассмотрим устойчивость электропривода.

В общем случае под устойчивостью системы ( в данном случае – электропривода )

понимают ее способность вернуться к прежнему или близкому к прежнему состоянию по-

сле кратковременногодействия на нее внешнего возмущающего воздействия ( рис. 2.9 ).

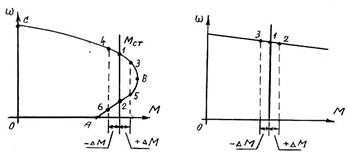
Рис. 2.9. Механические характеристики асинхронного двигателя ( а ) и двигателя параллельного возбуждения ( б )

В данном случае, под внешним возмущающим воздействием будем понимать изме-

нение исходного статического момента М 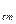на величину + Δ М или — Δ М.

Рассмотрим устойчивость работы привода в двух случаях:

1. в исходном состоянии двигатель работает в точке 1 на участке ВС своей механи-

2. в исходном состоянии двигатель работает в точке 2 на участке АВ.

Для упрощения объяснения механическую характеристику механизма изобразим в виде вертикальной прямой М .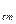

В первом случае асинхронный двигатель работает в точке 1 в установившемся ре-

Для этой точки справедливо равенство моментов двигателя М = М .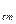

Если кратковременно увеличить статический момент на величину + Δ М, до значе

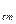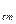ния М’ = М + Δ М, двигатель за счет саморегулирования перейдет из точки 1 в точку 3.

В этой точке наступит установившийся режим, т.к. момент двигателя увеличился до значения, равного возросшему моменту механизма.

Если скачкообразно убрать внешнее воздействие, т.е. статический момент механиз-

ма уменьшить до прежнего значения М 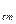, то электромагнитный момент двигателя в пер-

вый момент времени не изменится.

Последнее объясняется тем, что из-за инерции якоря его скорость не может изме-

ниться мгновенно, т.е. в первый момент останется такой, как в точке 3.

Поэтому ( см. логическую цепочку выше ) противоэлектродвижущая сила обмотки якоря, а значит, ток якоря и электромагнитный момент двигателя останутся прежними, как в точке 3.

Значит, электромагнитный момент двигателя в точке 3 окажется больше статиче-

ского момента механизма ( точка 1 ), поэтому двигатель станет разгоняться по участку

3 -1 своей механической характеристики, возвращаясь из точки 3 в точку 1.

На этом участке скорость двигателя увеличивается, а момент уменьшается.

Как только двигатель, уменьшая свой момент, вернется в точку 1, переходный про-

цесс закончится, т.к. в этой точке вновь наступит равновесие двух моментов – двигателя и механизма ( М = М ).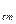

Наоборот, при уменьшении исходного статического момента на величину — Δ М электродвигатель автоматически, за счет саморегулирования, также уменьшит свой элект-

ромагнитный момент и перейдет из точки 1 в точку 4.

В этой точке наступит равновесие моментов двигателя и механизма ( М’ = М’ ).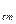

Если скачкообразно убрать внешнее воздействие, т.е. статический момент механиз-

ма увеличить до прежнего значения М 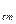, то электромагнитный момент двигателя в пер-

вый момент времени не изменится из-за инерции якоря ( см. саморегулирование ).

В результате этот момент ( точка 4 ) станет меньше тормозного статического ( точ-

ка 1 ), и двигатель станет тормозиться по участку 4 – 1 своей механической характеристи-

На этом участке момент двигателя увеличивается, и в точке 1 вновь наступит уста-

Таким образом, в любой точке отрезка ВС механической характеристики двигателя последний работает устойчиво.

Во втором случае асинхронный двигатель работает в точке 2 в установившемся ре-

Для этой точки справедливо равенство моментов двигателя М = М .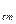

Если кратковременно увеличить статический момент на величину + Δ М, до значе-

ния 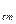М’ = М 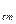+ Δ М, двигатель за счет саморегулирования перейдет из точки 1 в точку 5.

В этой точке наступит установившийся режим, т.к. момент двигателя увеличился до значения, равного возросшему моменту механизма.

Если скачкообразно убрать внешнее воздействие, т.е. статический момент механиз-

ма уменьшить до прежнего значения М 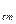, то электромагнитный момент двигателя М в первый момент времени не изменится, и он окажется больше тормозного статического.

Поэтому в последующие моменты времени двигатель станет разгоняться по участ-

ку 5- В -1 и в точке 1 вновь наступит равновесие моментов двигателя и механизма.

Таким образом, в рассмотренном случае двигатель не вернулся в точку 2 исходного режима, а перешел работать в точку 1 с повышенной против точки 2 скоростью.

Если же, начиная с точки 2, кратковременно уменьшить статический момент М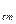

на величину — Δ М, двигатель перейдет за счет саморегулирования из точки 2 в точку 6, в которой наступит установившийся режим.

Если скачкообразно убрать внешнее воздействие, т.е. статический момент механиз-

ма увеличить до прежнего значения М 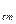, то электромагнитный момент двигателя М в пер

вый момент времени не изменится, и он окажется меньше тормозного статического.

Поэтому в последующие моменты времени двигатель станет тормозиться по участ-

ку 6 – А, и в точке А остановится и перейдет в режим стоянки под током.

Таким образом, и в этом случае двигатель не вернулся в точку 2 исходного режима,

а перешел в точку А с пониженной против точки 2 скоростью, равной нулю.

Таким образом, в любой точке отрезка АВ механической характеристики двигателя последний работает неустойчиво.

Получим условие устойчивости асинхронного двигателя.

На участке ВС ( устойчивая работа ) жесткость механической характеристики

β = 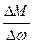0 ), например, при переходе из точки 1 в точку 3, скорость уменьшается ( Δω 0,

т.е. при увеличении момента М ( ΔМ > 0 ), например, при переходе из точки 2 в точку 5 скорость также увеличивается ( Δω > 0 ), и наоборот.

Таким образом, двигатель работает устойчиво на участке механической характери-

стики, где жесткость отрицательна ( β 0 ).

Более подробно устойчивость работы асинхронного двигателя рассматривается ниже ( см. §*** «Опрокидывание асинхронного двигателя» ).

Сравним устойчивость асинхронного двигателя и двигателя постоянного тока с па-

раллельным возбуждением ( рис. 2.9, б ).

Рассуждая аналогично, можно показать, что при увеличении статического момента

на величину + ΔМ двигатель постоянного тока перейдет из исходной точки 1 в точку 2, в которой наступит установившийся режим.

Если скачкообразно убрать внешнее воздействие, т.е. статический момент механиз-

ма уменьшить до прежнего значения М 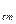, то электромагнитный момент двигателя М в первый момент времени окажется больше статического.

Поэтому в последующие моменты времени двигатель станет разгоняться по участ-

ку 2 – 1, и в точке 1 переходный процесс закончится.

В этой точке вновь наступит установившийся режим.

Наоборот, при уменьшении статического момента на величину – ΔМ двигатель пе-

рейдет из исходной точки 1 в точку 3, в которой наступит установившийся режим.

Если скачкообразно убрать внешнее воздействие, т.е. статический момент механиз-

ма увеличить до прежнего значения М 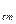, то электромагнитный момент двигателя М в пер

вый момент времени не изменится, и он окажется меньше тормозного статического.

Двигатель станет тормозиться по участку 3 – 1 своей механической характеристи-

На этом участке момент двигателя увеличивается.

В точке 1 вновь наступит установившийся режим.

Таким образом, двигатель с параллельным возбуждением работает устойчиво в лю

бой точке своей механической характеристики до момента остановки якоря.

При остановке якоря двигатель перейдет в режим короткого замыкания ( режим стоянки под током ). Этому режиму соответствует точка пересечения механической харак-

теристики электродвигателя с положительной полуосью оси моментов М.

Если, начиная с этой точки, увеличить активный статический момент ( в элекропри

водах ГПМ или ЯШУ увеличением веса груза или якоря с якорь-цепью, двигатель реверси

рует и станет увеличивать свой электромагнитный момент до те пор, пока последний не

сравняется с возросшим статическим моментом механизма. При наступлении равенства этих двух моментов вновь наступит установившийся режим тормозного спуска.

Определение устойчивости систем автоматического управления промышленными роботами

Введение

Необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия [1].

Постановка задачи

Теория просто и кратко

Анализ устойчивости системы по методу Михайлова сводится к построению характеристического многочлена замкнутой системы (знаменатель передаточной функции), комплексной частотной функции (характеристического вектора):

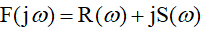(1)

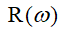где и 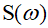– соответственно вещественная и мнимая части знаменателя передаточной функции, по виду которой можно судить об устойчивости системы.

Замкнутая САУ устойчива, если комплексная частотная функция , начинаясь на
стрелки начало координат, проходя последовательно n квадрантов, где n – порядок характеристического уравнения системы, т. е.

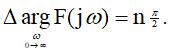(2)

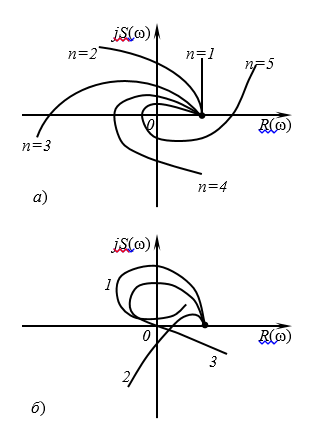
Рисунок 1. Амплитудно-фазовые характеристики (годографы) критерия Михайлова: а) – устойчивой системы; б) – неустойчивой системы (1, 2) и системы на границе устойчивости (3)

САУ электроприводом манипулятора промышленного робота (МПР)

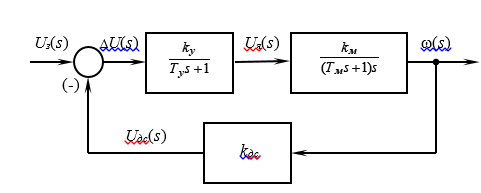
Рисунок 2 – Структурная схема САУ электроприводом МПР

Передаточная функция данной САУ имеет следующее выражение [2]:

(3)
где kу – коэффициент усиления усилителя, kм – коэффициент пропорциональности частоты вращения двигателя величине напряжения на якоре, Tу – электромагнитная постоянная времени усилителя, Tм – электромеханическая постоянная времени двигателя с учётом инерции нагрузки (по своим динамическим характеристикам двигатель представляет собой передаточную функцию последовательно соединённых инерционного и интегрирующего звеньев), kдс – коэффициент пропорциональности между входной и выходной величинами датчика скорости, K – коэффициент усиления главной цепи: .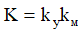

Численные значения в выражение передаточной функции следующие:

K = 100 град / (В∙с); kдс = 0,01 В / (град∙с); Tу = 0,01 с; Tм = 0,1с.

Далее запишем характеристический многочлен замкнутой системы

заменив s на :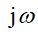
(4)

Решение на Python

Здесь следует отметить, что подобные задачи на Python ещё никто не решал, во всяком случае я не нашёл. Это было связано с ограниченными возможностями работы с комплексными числами. С появлением SymPy можно сделать следующее:

Где I мнимая единица, w- круговая частота, T1= Tу = 0.01 ,T2= Tм = 0.1
Получим развёрнутое выражение для многочлена:

Характеристический многочлен замкнутой системы –
-I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1

Сразу видим, что многочлен третьей степени. Теперь получим мнимую и действительную части в символьном отображении:

Действительная часть Re= -T1*w**2 — T2*w**2 + 1
Мнимая часть Im= -T1*T2*w**3 + w

Сразу видим вторую степень действительной части и третью мнимой. Подготовим данные для построения годографа Михайлова. Введём численные значения для T1 и T2, и будем менять частоту от 0 до 100 с шагом 0.1 и построим график:

Из графика не видно, то годограф начинается на действительной положительной оси. Нужно изменить масштабы осей. Приведу полный листинг программы:

Характеристический многочлен замкнутой системы — -I*T1*T2*w**3 — T1*w**2 — T2*w**2 + I*w + 1
Действительная часть Re= -T1*w**2 — T2*w**2 + 1
Мнимая часть Im= -T1*T2*w**3 + w

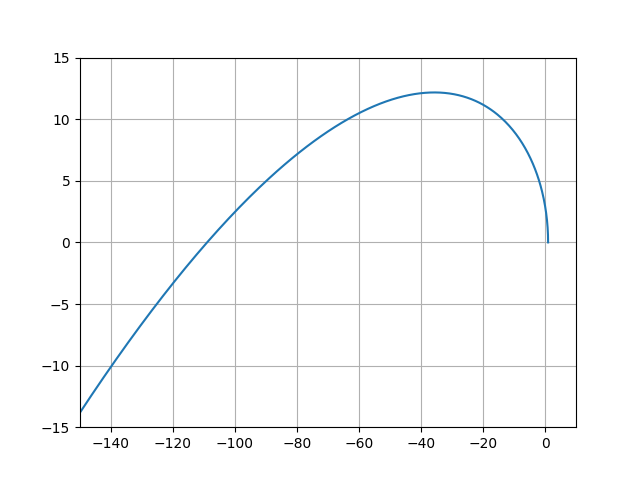
Теперь уже видно, что годограф начинается на действительной положительной оси. САУ устойчива, n=3, годограф совпадает с приведённым на первом рисунке.

Дополнительно убедится в том, что годограф начинается на действительной оси можно дополнив программу следующим кодом для w=0:

Начальная точка М(1,0)

САУ сварочного робота

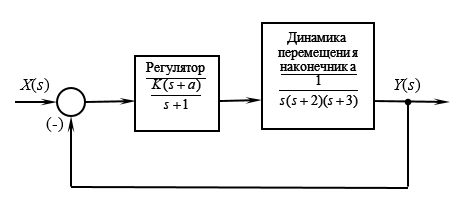
Рисунок 3. Структурная схема САУ позиционированием НСУ

Характеристическое уравнение данной САУ будет иметь вид [1]:

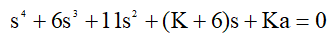
где K – варьируемый коэффициент усиления системы, a – определённая положительная константа. Численные значения: K = 40; a = 0,525.

Далее путём замены s на 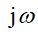, получим функцию Михайлова:
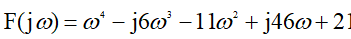(5)

Решение на Python

Характеристический многочлен замкнутой системы — w**4 — 6*I*w**3 — 11*w**2 + 46*I*w + 21
Начальная точка М(21,0)
Действительная часть Re= w**4 — 11*w**2 + 21
Мнимая часть Im= -6*w**3 + 46*w

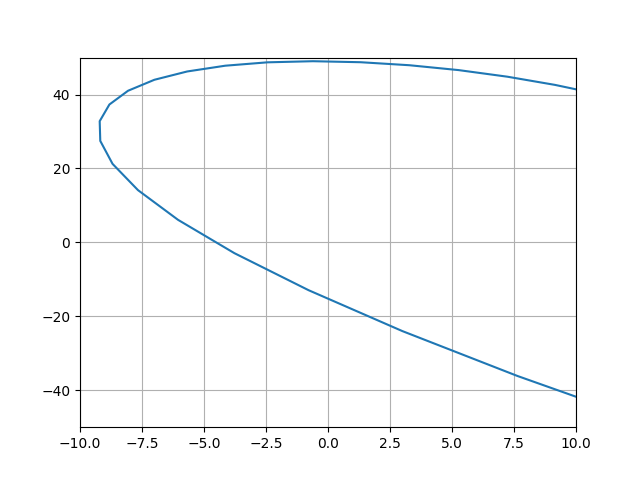
Построенный годограф Михайлова, начинаясь на вещественной положительной оси (М (21,0)), огибает в положительном направлении начало координат, проходя последовательно четыре квадранта, что соответствует порядку характеристического уравнения. Значит, данная САУ позиционированием НСУ – устойчива.

Выводы

При помощи модуля SymPy Python получен простой и наглядный инструмент для решения задач расчёта устойчивости систем автоматического управления, что является обязательным условием работоспособности любого промышленного робота и манипулятора.

Устойчивость автомобиля. Опрокидывание и его причины

Устойчивость – это совокупность свойств, определяющих критические параметры по устойчивости движения и положения автомобильного транспортного средства (АТС) или его звеньев.

Признаком потери устойчивости является скольжение АТС или его опрокидывание. В зависимости от направления скольжения или опрокидывания АТС различают поперечную и продольную устойчивость.

Во время движения автомобиль имеет инерцию, а в момент начала поворота, помимо центробежной силы возникает дополнительная поперечная сила (составляющая сила инерции), направленная в том же направлении, что и центробежная сила. При очень большой скорости движения и резком повороте (поперечная составляющая сила инерции и центробежная) суммарная сила может привести даже к опрокидыванию автомобиля.

Поперечная сила С стремится нарушить устойчивость автомобиля, а сила G стремится удержать его в устойчивом положении. Колеса образуют крайние опоры автомобиля, а центр тяжести (ЦТ) расположен на равном удалении от правого и левого колес и на определенной высоте hn от поверхности дороги. Чем выше центр тяжести и уже колея автомобиля, тем больше он подвержен опасности опрокидывания.

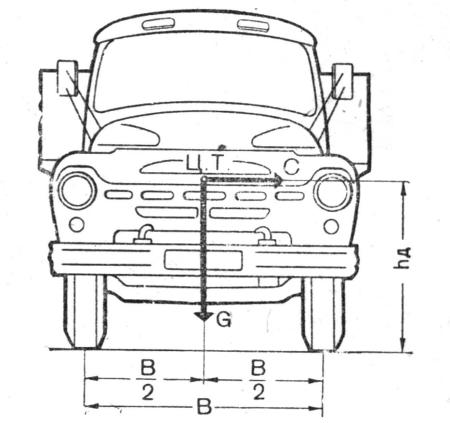
Рис. Схема сил влияющих на поперечную устойчивость автомобиля

Опрокидывание автомобиля

Опрокидывание автомобиля может произойти как в продольной, так и в поперечной плоскости.

Опрокидывание в продольной плоскости относительно задней оси происходит в момент, когда сила давления передних колес на дорогу уменьшается до нуля. Практически до начала опрокидывания наступает буксование колес на подъеме, автомобиль сползает назад вследствие недостаточного сцепления колес с дорогой.

Возможно переворачивание автомобиля вперед при резком торможении на крутом спуске, если автомобиль имеет короткую базу и высоко расположенный центр тяжести. В данном примере возникшая сила инерции складываясь с горизонтальной составляющей силы веса, дает результирующую силу, которая выходит за пределы опорной площади передней оси автомобиля. Известны случаи опрокидывания автомобиля назад, когда при движении задним ходом автомобиль съезжает в овраг, реку и т. п.

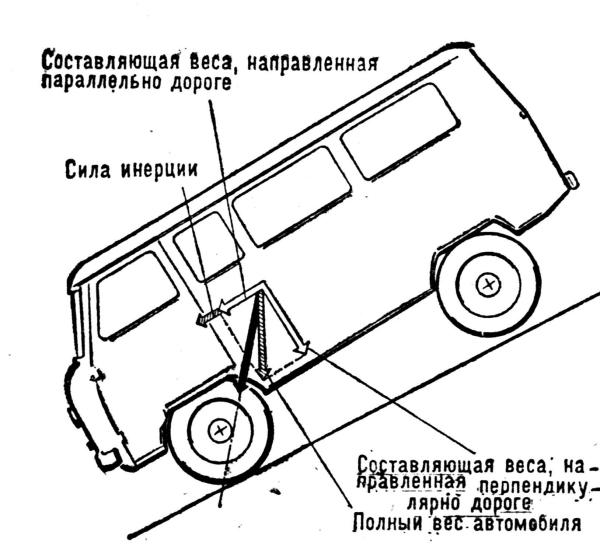
Рис. Продольное опрокидывание автомобиля на спуске во время торможения

При движении автомобиля по дороге, имеющей поперечный уклон, возникает боковая сила, равная поперечной составляющей от веса автомобиля. Эта сила может вызвать опрокидывание автомобиля или его скольжение вбок. Устойчивость автомобиля к опрокидыванию в этом случае зависит от колеи автомобиля высоты расположения центра тяжести и угла поперечного наклона дороги.

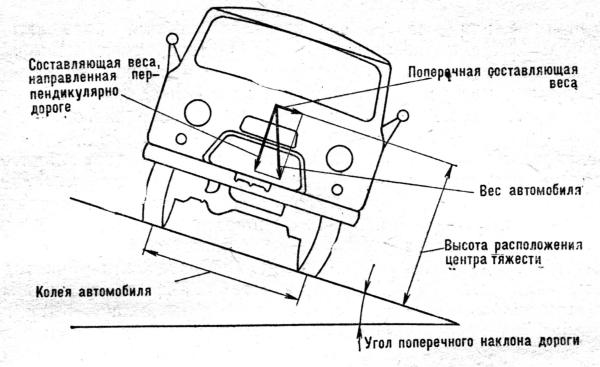
Рис. Схема сил, действующих на автомобиль при движении на дороге, имеющей поперечный уклон

Чем выше расположен груз, тем больше высота расположения центра тяжести, следовательно, тем вероятнее опрокидывание грузового автомобиля. Чем шире колея автомобиля, тем более устойчив автомобиль как при движении на повороте, так и при движении по дороге, имеющей поперечный уклон.

Опрокидывание автомобиля в поперечной плоскости, т.е. вбок, может произойти под действием центробежной силы на повороте, при резком повороте рулевого колеса на большой скорости, сильном боковом наклоне и вследствие неправильного закрепления груза в кузове.

Неправильная укладка груза в кузове может значительно изменить положение центра тяжести, сместив его как вбок, так и вверх. Характерным примером может служить цистерна, не заполненная целиком жидким грузом. Под влиянием центробежной силы жидкий груз смещается к одной стороне цистерны, центр тяжести смещается вверх и в сторону, а сила тяжести, удерживающая автомобиль от опрокидывания, действует уже не по оси автомобиля а смещается в сторону перемещения центра тяжести.

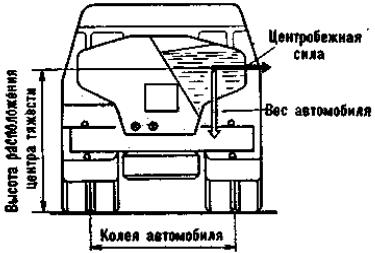
Рис. Смещение центра тяжести жидкого груза под действием центробежной силы

Причины опрокидывания автомобиля

• при высокой скорости движения на крутых поворотах, на неблагоустроен­ных дорогах, где поперечный уклон направлен в сторону, противоположную повороту
• вследствие резкого прекращения бокового заноса при толчке заднего колеса о камень или другое препятствие
• при резком повороте рулевого колеса на большой скорости
• при неравномерном расположении груза в кузове автомобиля или его перемещении на повороте

Чтобы избежать опрокидывания, нужно на опасных участках дороги снизить скорость, плавно повернуть рулевое колесо, плавно тормозить, равномерно разместить и хорошо закрепить груз в кузове автомобиля.